Fdzfgy

(animasjon)

Ein oktaeder bretta ut i ei todimensjonal flate.

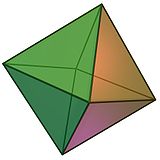
Oktaeder er eit polyeder med åtte sideflater, men vanlegvis vert det meint eit regulært oktaeder: ein platonsk lekam sett saman av åtte trekanta sideflater. Desse overflatene er likesida trekantar. I tillegg har den seks hjørne og tolv kantar.

Areal og volum |

Viss a{displaystyle a} i eit regulært oktaeder er kant, kan arealet og volumet reknast ut slik:

A=23a2≈3.46410162a2{displaystyle A=2{sqrt {3}}a^{2}approx 3.46410162a^{2}}

V=132a3≈0.471404521a3{displaystyle V={frac {1}{3}}{sqrt {2}}a^{3}approx 0.471404521a^{3}}

Radius |

Viss a{displaystyle a} i eit regulært oktaeder er kant, er radiusen av ei kule som akkurat fyller ut hele figuren:

ru=a22≈0.7071067⋅a{displaystyle r_{u}={frac {a}{2}}{sqrt {2}}approx 0.7071067cdot a}

Radiusen av den største kula som kan innskrivast i det er:

ri=a66≈0.4082482⋅a{displaystyle r_{i}={frac {a}{6}}{sqrt {6}}approx 0.4082482cdot a}

Midtradiusen, dvs. radiusen av ei kule der flata rører midten av kvar kant, er:

rm=a2=0.5⋅a{displaystyle r_{m}={frac {a}{2}}=0.5cdot a}

Avkuttingssekvens |

Tetraeder

Avkutta tetraeder

Oktaeder

Avkutta tetraeder

Tetraeder

Sjå òg |

• Platonsk lekam


• Trekant