Polynom
Eit polynom er i matematikk ein sum av ei endeleg mengd ledd der kvart ledd er ein konstant multiplisert med ein eller fleire variablar opphøgd i positive heiltalseksponentar. Polynomet er definert berre ved hjelp av operasjonane addisjon, subtraksjon og multiplikasjon. I dei følgjande døma er det vist eit polynom i éin variabel x og eit polynom i to variable x og y:
- 2x3+5x2−2{displaystyle 2x^{3}+5x^{2}-2,}
- 2x2y2−3y2+5xy−2{displaystyle 2x^{2}y^{2}-3y^{2}+5xy-2,}
Konstantane som inngår kallast òg koeffisientar i polynomet.
Første delen av namnet polynom kjem frå gresk polus som tyder fleire. Det er uklart om andre delen er avleidd frå gresk nomos = reglar eller latin nomen = namn. Eit polynom med berre éit ledd kan kallast eit monom, medan eit binom og eit trinom har høvesvis to og tre ledd.
Likningar som involverer berre polynom kallast polynomlikningar, og andregradslikninga er eit velkjent døme. Funksjonar definert ved eit polynom kallast naturleg nok polynomfunksjonar.
Polynom har eit stort bruksområde i matematikk, og polynom opptrer i nær sagt alle fagområde der matematikk brukast. Studiet av polynomlikningar og røtene har tradisjonelt vore ein viktig del av algebra. Den enkle forma gjer at polynom ofte blir brukt for å gje ei tilnærma riktig skildring av meir komplekse samanhengar. Polynom er viktige i mange numeriske berekningsmetodar, til dømes endeleg-element-metoden.
Innhaldsliste
1 Fundamentale omgrep
2 Polynomfunksjonar
2.1 Polynomfunksjonar i éin variabel
2.2 Vektorrom av polynomfunksjoner
3 Polynomlikningar
3.1 Fundamentalteoremet i algebra
3.2 Løysing av polynomlikningar
4 Funksjonstilnærming med polynom
4.1 Tilnærming ved Taylorutvikling
4.2 Ortogonale polynom
4.3 Splinefunksjonar
5 Generaliseringar
5.1 Trigonometriske polynom
5.2 Matrisepolynom
6 Bakgrunnsstoff
7 Kjelder
Fundamentale omgrep |
Eit ledd i eit polynom har grad n dersom summen av eksponentane til variablane i leddet er lik n. Grada til polynomet er lik den største grada til alle av ledda. Det første dømet i introduksjonen har dermed grad lik tre, medan det andre har grad fire. Eit polynom av grad 2 blir kalla både eit andregradspolynom og eit kvadratisk polynom, medan eit kubisk polynom har grad 3.
Eit polynom av grad n er komplett dersom det inneheld ledd av alle potensar mindre eller lik n i variablane. Eit komplett tredjegrads polynom i éin variabel har fire ledd, medan eit komplett tredjegrads polynom i to variable har 10 ledd, som i det følgjande dømet:
- 2x3+3y3+x2y+6xy2−3xy+5x2−y2−2x+y+7{displaystyle 2x^{3}+3y^{3}+x^{2}y+6xy^{2}-3xy+5x^{2}-y^{2}-2x+y+7,}
Eit n-te-grads polynom i éin variabel er monisk dersom koeffisienten føre leddet med eksponent n er lik 1.
Eit polynom i fleire variable er symmetrisk dersom ein permutasjon av variablane ikkje endrar polynomet. Eit polynom p(x,y) i to variable er altså symmetrisk dersom
- p(x,y)=p(y,x){displaystyle p(x,y)=p(y,x),}
Eit polynom i fleire variable er homogent i grad n dersom alle ledda har grad n.
Polynomfunksjonar |
Ein polynomfunksjon er ein funksjon som evaluerer verdien av eit polynom. Omgrepa polynom og polynomfunksjon blir ofte brukt om kvarandre, men i abstrakt algebra er skilnaden mellom desse omgrepa viktig.
Polynomfunksjonar har mange attraktive matematiske eigenskapar, dei er blant anna kontinuerlege og glatte. Polynom er både deriverbare og integrerbare, og resultatet av desse operasjonane er òg polynom.
Polynomfunksjonar i éin variabel |
Den generelle forma for eit n-te-grads polynom i éin variabel er
- p(x)=anxn+an−1xn−1+...+a1x+a0{displaystyle p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0},}
Her er ai (i = 1,...,n) koeffisientane i polynomet, og x er argumentet i funksjonen.
Polynomfunksjonar kan vere reelle eller komplekse, alt etter korleis koeffisientane og variablane er definerte.
Horners regel eller Horner-algoritmen er ein effektiv måte for berekning av polynomfunksjonar.
Grafen til ein polynomfunksjon av grad éin er ei rett linje. Andregradspolynomet har ein graf som blir kalla ein parabel. Døme på polynom-grafar er vist under.
 Andregradspolynom: f(x) = x2 - x - 2 = (x+1)(x-2) | 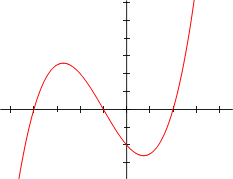 Tredjegradspolynom: f(x) = x3/5 + 4x2/5 - 7x/5 - 2 = 1/5 (x+5)(x+1)(x-2) |
 Fjerdegradspolynom: f(x) = 1/14 (x+4)(x+1)(x-1)(x-3) + 0.5 |  Femtegradspolynom : f(x) = 1/20 (x+4)(x+2)(x+1)(x-1)(x-3) + 2 |
Vektorrom av polynomfunksjoner |
Summen av to polynom er òg eit polynom. Multipliserer ein eit polynom med eit reelt eller eit komplekst tal, så er resultatet òg eit polynom. Til saman gjer dette at ein kan definere ei rekkje vektorrom danna frå ein basis av polynomfunksjonar. Som ein del av definisjonen inngår òg det såkalla nullpolynomet, definert ved
- p(x)=0{displaystyle p(x)=0,}
Som eit døme kan ein definere basisfunksjonane
- p0(x)=1{displaystyle p_{0}(x)=1,}
- pi(x)=xii=1,...,n{displaystyle p_{i}(x)=x^{i}quad i=1,...,n,}
Eit vilkårleg n-te-grads polynom kan då skrivast som
- p(x)=anpn(x)+an−1pn−1(x)+...+a1p1(x)+a0p0(x){displaystyle p(x)=a_{n}p_{n}(x)+a_{n-1}p_{n-1}(x)+...+a_{1}p_{1}(x)+a_{0}p_{0}(x),}
Koordinatvektoren er gjeven ved
- (an,an−1,...,a1,a0){displaystyle (a_{n},a_{n-1},...,a_{1},a_{0}),}
Vektorrommet av polynom opp til grad n er eit (n+1)-dimensjonalt vektorrom med same struktur som Rn+1, det vil sei isomorft med Rn+1.
Polynomlikningar |
Ei likning der eit polynom er sett lik null blir kalla ei polynomlikning. Andregradslikninga er eit velkjent døme.
Fundamentalteoremet i algebra |
Ifølge fundamentalteoremet i algebra har ei kompleks n-te-grads polynomlikning av éin variabel eksakt n røter, når multiplisiteten til rota er rekna med. Dersom røtene xi (i = 1,...,n) er kjente, så kan polynomet skrivast på forma
- pn(x)=an(x−x1)(x−x2)…(x−xn){displaystyle p_{n}(x)=a_{n}(x-x_{1})(x-x_{2})dots (x-x_{n}),}
Overføring av polynomet til ei slik form blir kalla faktorisering av polynomet. Røtene treng ikkje vere reelle, sjølv om koeffisientane i polynomet er relle. Kvadratsetningane er døme på faktorisering av andregradspolynom.
Løysing av polynomlikningar |
Løysing av andregradslikningar har vore studert sidan babylonartida, 1600 år f.Kr. Den generelle forma for løysinga av andregradslikninga ved den såkalla ABC-formelen er velkjend. Òg løysing av tredjegradslikningar og fjerdegradslikningar kan uttrykkjast på slutta form ved hjelp av aritmetiske operasjonar og rotutdragingar. Cardanos metode gjev løysinga av den generelle tredjegradslikninga, medan Ferraris metode kan brukast for fjerdegradslikningar.
I 1824 viste Niels Henrik Abel at dette ikkje er mogleg for løysinga av den generelle polynomlikninga av grad større eller lik fem, og dette resultatet er kjent som Abel-Ruffini-teoremet.
Merk at fundamentalteoremet viser at òg femtegradslikningar alltid har løysingar, - ein kan berre ikkje alltid uttrykkje desse på slutta form.
I Galoisteori studerer ein relasjonar mellom røtene i polynomlikningar.
Funksjonstilnærming med polynom |
Weierstrass’ approksimasjonsteorem, kalla opp etter Karl Weierstrass, seier at ein vilkårleg kontinuerleg funksjon definert på eit intervall [a,b] kan tilnærmast uniformt så nøyaktig ein berre vil ved hjelp av polynomfunksjonar. Resultatet blir òg kalla Stone-Weierstrass-teoremet.
Formelt kan ein uttrykkje dette, som følgjer: Gjeve ein kontinuerleg funksjon f(x) definert på intervallet [a,b] og eit vilkårleg positivt tal ϵ{displaystyle epsilon }. Då eksisterer det eit polynom p(x) slik at
- maxx∈[a,b]|f(x)−p(x)|<ϵ{displaystyle max _{xin [a,b]}|f(x)-p(x)|<epsilon ,}
Tilnærming ved Taylorutvikling |
Ein funksjon som er uendeleg mange gonger deriverbar blir ofte tilnærma ved hjelp av eit polynom definert ved taylorrekkja til funksjonen. I eit område nær argumentet x = c er tilnærminga gjeven ved
- f(x)≈∑i=1n1i!f(i)(c)(x−c)i{displaystyle f(x)approx sum _{i=1}^{n}{1 over i!}f^{(i)}(c)(x-c)^{i}}
Jo høgare orden i polynomet ein bruker, jo betre er tilnærminga. I det følgjande dømet er feilen i tilnærminga mindre enn 0,000003 i intervallet [-1,1]:
- sin(x)≈x−x33!+x55!−x77!{displaystyle sin left(xright)approx x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}},}
Ortogonale polynom |
I vektorrom av polynom kan ein definere mange alternative indreprodukt, for polynom av éin variabel ofte gjeven på den følgjande forma
- <p1(x),p2(x)> =∫abw(x)p1(x)p2(x)dx{displaystyle <p_{1}(x),p_{2}(x)> =int _{a}^{b}w(x)p_{1}(x)p_{2}(x)dx,}
To polynom er ortogonale dersom indreproduktet er lik null. Ulike definisjonar av vektfunksjonen w(x) vil føre til ulike definisjonar av ortogonale polynom, og det eksisterer mange typar som alle har mange bruksområde der dei brukast til å tilnærme meir generelle funksjonar og til interpolasjon. Ulike klasser av ortogonale polynom er typisk oppkalla etter ein matematikar som har medverka til utviklinga av teorien for desse:
Chebyshevpolynom, oppkalla etter Pafnuty Chebyshev
Hermitske polynom, oppkalla etter Charles Hermite
Jacobipolynom, oppkalla etter Carl Gustav Jacob Jacobi
Laguerrepolynom, oppkalla etter Edmond Laguerre
Legendrepolynom, oppkalla etter Adrien-Marie Legendre
Splinefunksjonar |
Splinefunksjonar er konstruert ved å setje saman polynom definert på del-intervall, og desse funksjonane er svært nyttige til funksjonstilnærmingar.
Generaliseringar |
Polynom kan genraliserast ved å erstatte eit argument x med ein meir kompliserte funksjon eller ein annan datatype.
Trigonometriske polynom |
Ein trigonometrisk polynom er eit uttrykk på forma
- a0+∑i=1n[aisin(ix)+bicos(ix)]{displaystyle a_{0}+sum _{i=1}^{n}left[a_{i}sin(ix)+b_{i}cos(ix)right],}
Matrisepolynom |
Eit matrisepolynom er eit uttrykk på forma
- anMn+an−1Mn−1+...+a1M+a0{displaystyle a_{n}M^{n}+a_{n-1}M^{n-1}+...+a_{1}M+a_{0},}
der M er ei kvadratisk matrise, slik at matrisemultiplikasjon er definert.
Bakgrunnsstoff |
- Opphavet til namnet polynom, på engelsk
Kjelder |
Denne artikkelen bygger på «Polynom» frå Wikipedia på bokmål, den 15. januar 2012.
- Wikipedia på bokmål oppgav desse kjeldene:
Hans-Frederik Aas (1974). Forelesningsreferater i matematisk analyse, del I. Bergen: Matematisk institutt, Universitetet i Bergen.
Ronald Douglas Milne (1980). Applied functional analysis, an introductory treatment. London: Pitman Publishing Limited. ISBN 0-273-08404-6.
Steven Schwartzman (1994). The words of mathematics. An etymological dictionary of mathematical terms used in English. Washington, DC: The Mathematical Association of America. ISBN 0-88385-511-9.
|












![{displaystyle max _{xin [a,b]}|f(x)-p(x)|<epsilon ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/570ddfad61c1c7b0a73613bb370b5283d5c57302)



![{displaystyle a_{0}+sum _{i=1}^{n}left[a_{i}sin(ix)+b_{i}cos(ix)right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cab9776f765fc6d7523ba41be26b2081b031f152)
