Effektiv temperatur
Den effektive temperaturen til ein lekam som ei stjerne eller ein planet er den temperaturen ein svart lekam ville ha om han strålte ut same mengd elektromagnetisk stråling.[1] Effektiv temperatur vert ofte nytta som eit temperaturestimat til ein lekam når ein ikkje kjenner emissivitetskurva (som ein funksjon av bølgjelengd) til lekamen.
Innhaldsliste
1 Stjerne
2 Planet
3 Sjå òg
4 Kjelder
5 Bakgrunnsstoff
Stjerne |
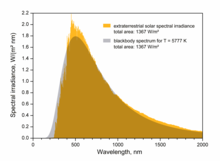
Den effektive temperaturen til sola (5777 K) er temperaturen ein svart lekam på same storleik må ha for å stråle ut den same mengda elektromagnetisk stråling.
Den effektive temperaturen til ei stjerne er temperaturen til ein svart lekam med same luminositet per overflateareal (FBol{displaystyle {mathcal {F}}_{mathrm {Bol} }}) som stjerna og som er definert med hjelp av Stefan–Boltzmann-lova FBol=σTeff4{displaystyle {mathcal {F}}_{mathrm {Bol} }=sigma T_{mathrm {eff} }^{4}}. Merk at den totale (bolometriske) luminositeten til ei stjerne då er L=4πR2σTeff4{displaystyle L=4pi R^{2}sigma T_{mathrm {eff} }^{4}}, der R{displaystyle R} er stjerneradiusen.[2] Definisjonen på stjerneradiusen er ikkje enkel å finne. Ein strengare definisjon er at den effektive temperaturen samsvarar med temperaturen ved ein radius definert av Rosseland optiske tjukkleik.[3][4] Den effektive temperaturen og den bolometriske luminositeten er to grunnleggande fysiske parametrar som ein treng for å plassere ei stjerne på HR-diagrammet. Både effektiv temperatur og bolometrisk luminositet er avhengige av den kjemiske samansettinga til ei stjerne.
Den effektive temperaturen til sola vår er rundt 5780 kelvin (K).[5][6]
Stjerner har faktisk ein temperaturgradient som går frå kjernen deira og opp til atmosfæren. Kjernetemperaturen i sola, altså temperaturen i midten av sola der kjernereaksjonane skjer, er estimert til å vere 15 000 000 K.
Fargeindeksen til ei stjerne indikerer temperaturen til stjerna, frå særs kald (relativt sett), som er raude M-stjerner som stråler ut mykje infraraud stråling til dei særs blå O-stjernene som hovudsakleg stråler ultrafiolett. Den effektive temperaturen til ei stjerne indikerer varmemengda som stjerna stråler ut per overflateareal. frå den varmaste flata til den kjøligaste er stjernetypane O, B, A, F, G, K og M.
Ei raud stjerne kan vere ein liten raud dverg, ei stjerne med svak energiproduksjon og ei lita overflate, eller ein oppsvulma gigant eller til og med supergigant som Antares eller Betelgeuse, som produserer store energimengder, men som må passere gjennom ei flate som er så stor at stjerna stråler ut lite energi per overflateareal. Ei stjerne i midten av spektrumet, som den beskjedne sola eller den store Capella stråler meir varme per overflateareal enn ei svak raud dvergstjerne eller dei oppsvulma supergigantane, men mykje mindre enn kvite eller blå stjerner som Vega or Rigel.
Planet |
Den effektive temperaturen til ein planet kan reknast ut ved å sjå på strålinga som treffer planeten og strålinga som planeten stråler ut med temperaturen til ein svart lekam T.
Om ein har ein planet med avstand D frå stjerna, luminositet L.
Ved å tenkje seg at stjerna stråler isotropisk og at planeten er langt borte frå stjerna, så kan krafta planeten absorberer handsamast som om planeten er ein disk med radius r, som tar imot noko av krafta spreidd over kuleflate med radius D. Vi let òg planeten reflektere noko av den innkommande strålinga ved å nytte ein parameter kalla albedo. Ein albedo på 1 tyder at all strålinga vert reflektert, og ein albedo på 0 at all strålinga vert absorbert. Uttrykket for den absorberte strålinga vert då:
Pabs=Lr2(1−A)4D2{displaystyle P_{mathrm {abs} }={frac {Lr^{2}(1-A)}{4D^{2}}}}
Ein tenkjer seg vidare at heile planeten har same temperatur T, og at planeten stråler som ein svart lekam. Stefan–Boltzmann-lova gjev ei uttrykk for strålinga som planeten sender ut:
Prad=4πr2σT4{displaystyle P_{mathrm {rad} }=4pi r^{2}sigma T^{4}}
Ved å rekne ut desse to uttrykka og omarrangere dei, får ein eit uttrykk for den effektive temperaturen:
T=(L(1−A)16πσD2)14{displaystyle T=left({frac {L(1-A)}{16pi sigma D^{2}}}right)^{tfrac {1}{4}}}
Merk at radiusen til planeten er vorte kansellert bort frå det siste uttrykket.
Den effektive temperaturen for Jupiter er 112 K og 51 Pegasi b (Bellerophon) er 1258 K. Den faktiske temperaturen er avhengig av albedo, atmosfære og indre varme. Den faktiske temperaturen ein har frå spektroskopisk analyse for HD 209458 b (Osiris) er 1130 K, medan svartlekamtemperaturen er 1359 K.
Den indre varmen på Jupiter er 40 K, og i lag med den effektive temperaturen på 112 K vert den faktiske temperaturen 152 K (-121 ºC).
Sjå òg |
- Fargetemperatur
- Lysstyrketemperatur
Kjelder |
Denne artikkelen bygger på «Effective temperature» frå Wikipedia på engelsk, den 3. februar 2010.
Wikipedia på engelsk oppgav desse kjeldene:
↑ Archie E. Roy, David Clarke (2003). Astronomy. CRC Press. ISBN 9780750309172.
↑ Tayler, Roger John (1994). The Stars: Their Structure and Evolution. Cambridge University Press. s. 16. ISBN 0521458854.
↑ Böhm-Vitense, Erika. Introduction to Stellar Astrophysics, Volume 3, Stellar structure and evolution. Cambridge University Press. s. 14.
↑ Baschek, The parameters R and Teff in stellar models and observations
↑ «Section 14: Geophysics, Astronomy, and Acousticse». Handbook of Chemistry and Physics (88 utg.). CRC Press. More than one of|section=og|chapter=specified (hjelp)
↑ Jones, Barrie William (2004). Life in the Solar System and Beyond. Springer. s. 7. ISBN 1852331011.
Bakgrunnsstoff |
- Effektiv temperaturskala for solliknande stjerner
- Overflatetemperaturen til planetar
- Planettemperaturkalkulator






